Aquí tenemos 2 ejemplos en la aplicación de algoritmos recursivos:
SUCESION DE fibonacci
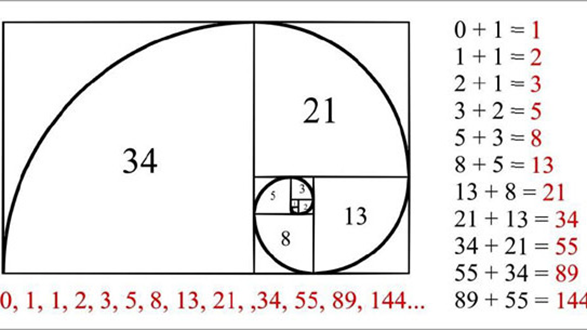
La sucesión de Fibonacci es conocida desde hace miles de años, pero fue
Fibonacci (Leonardo de Pisa) quien la dio a conocer al utilizarla para resolver
un problema.
El primer y segundo término de la sucesión son
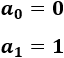
Los siguientes términos se obtienen sumando los dos términos que les preceden:
El tercer término de la sucesión es
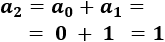
El cuarto término es
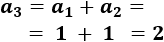
El quinto término es
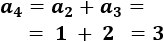
El sexto término es
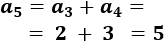
El -ésimo término es
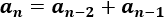
EJERCICIO EN JAVA
TORRES DE HANOI
El fin de las Torres de Hanoi es trasladar la
torre de discos a lo largo de tres varillas, desde la configuración inicial a
una configuración final indicada. Esta torre està fraccionada en bloques o
discos, los cuales deberá mover para restaurar de nuevo la torre en su posición
final.
La segunda varilla consiste en una torre de
“apoyo” que le permite colocar los discos de manera temporal. No obstante, uno
de los requerimientos de la prueba es que debe realizar el menor número de
movimientos posible y con el menor número de fallos.
EJERCICIO EN JAVA ejercicio realisado por ing. José Reynaldo Molina Menjívar.
package torreshanoi;
/**
*
* @author NormanGhost
*/
public class
TorresHanoi {
public static void main(String[] args) {
System.out.print ("Torres de
hanoi");
TorresHanoi objHanoi = new
TorresHanoi();
objHanoi.torresHanoi (3,1,2,3);
System.out.println("juego
Finalisado... XD");
}
//creando metodo recursivo para solucionar la torre de hanoi
public void torresHanoi(int discos , int torre1 , int
torre2 , int torre3){
if
(discos==1){
System.out.println("Mover disco de torre "+torre1+" a
torre "+torre3);
}else{
torresHanoi(discos-1,torre1,torre3,torre2);
System.out.println("Mover disco de torre "+torre1+" a
torre "+torre3);
torresHanoi(discos-1,torre2,torre1,torre3);
}
}
}
Entrada: Tres pilas de números origen,
auxiliar, destino, con la pila origen ordenadaSalida: La pila destino
1. si
origen entonces
1. mover el disco 1 de pila origen a la
pila destino (insertarlo arriba de la pila destino)
2. terminar
2. si
no
1. hanoi( ,origen,destino, auxiliar) //mover todas las fichas menos la más
grande (n) a la varilla auxiliar
3. mover
disco n a destino //mover la
ficha grande hasta la varilla final
4. hanoi
(auxiliar, origen, destino) //mover todas las fichas restantes, 1…n–1, encima
de la ficha grande (n)
5. terminar



No hay comentarios.:
Publicar un comentario